Physics Simulation Help Using Python Is really hard to make it from your end. Our specialists will provide valuable tips and resources for utilizing Python to develop physics simulations. You’ll receive exclusive, detailed guidance to enhance your work. Connect with our Python experts to assist you in resolving your simulation challenges. Share your project details with us for optimal results in your physics simulations. Carrying out a physics simulation with Python is an intriguing as well as challenging process that must be accomplished through employing suitable methods and tools. In order to conduct this process by means of Python, we suggest a few instances and approaches:
Significant Libraries for Physics Simulations
- NumPy: For numerical computations, NumPy is considered as a major library.
- SciPy: Highly innovative scientific computing functions are offered by SciPy, and it specifically develops on NumPy.
- Matplotlib: It is more suitable for data plotting and visualization.
- SymPy: This library is generally employed for symbolic mathematics.
- VPython: 3D visualization of physical frameworks is facilitated by VPython.
- PyBullet: For simulations of firm body dynamics, PyBullet is examined as a physics engine.
- Pygame: To develop communicative games and simulations, this library is more helpful.
Sample Physics Simulations
- Simple Harmonic Motion
import numpy as np
import matplotlib.pyplot as plt
# Parameters
mass = 1.0
k = 10.0 # spring constant
omega = np.sqrt(k / mass) # angular frequency
A = 1.0 # amplitude
T = 2 * np.pi / omega # period
time = np.linspace(0, 3 * T, 1000)
# Position as a function of time
position = A * np.cos(omega * time)
# Plot the motion
plt.plot(time, position)
plt.title(‘Simple Harmonic Motion’)
plt.xlabel(‘Time (s)’)
plt.ylabel(‘Position (m)’)
plt.grid(True)
plt.show()
- Projectile Motion
import numpy as np
import matplotlib.pyplot as plt
# Initial conditions
v0 = 50 # initial velocity (m/s)
angle = 45 # launch angle (degrees)
g = 9.81 # acceleration due to gravity (m/s^2)
angle_rad = np.radians(angle)
# Time of flight, maximum height, and range
T = 2 * v0 * np.sin(angle_rad) / g
H = (v0 ** 2) * (np.sin(angle_rad) ** 2) / (2 * g)
R = (v0 ** 2) * np.sin(2 * angle_rad) / g
# Time intervals
t = np.linspace(0, T, num=500)
# Trajectory equations
x = v0 * np.cos(angle_rad) * t
y = v0 * np.sin(angle_rad) * t – 0.5 * g * t**2
# Plot the trajectory
plt.plot(x, y)
plt.title(‘Projectile Motion’)
plt.xlabel(‘Distance (m)’)
plt.ylabel(‘Height (m)’)
plt.grid(True)
plt.show()
- Pendulum Simulation
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Parameters
g = 9.81 # acceleration due to gravity (m/s^2)
L = 1.0 # length of the pendulum (m)
theta0 = np.pi / 4 # initial angle (radians)
omega0 = 0.0 # initial angular velocity (rad/s)
# Differential equation
def pendulum_equation(y, t, L, g):
theta, omega = y
dydt = [omega, -g / L * np.sin(theta)]
return dydt
# Initial conditions
y0 = [theta0, omega0]
# Time points
t = np.linspace(0, 10, 250)
# Solve ODE
solution = odeint(pendulum_equation, y0, t, args=(L, g))
theta, omega = solution.T
# Plot the results
plt.plot(t, theta)
plt.title(‘Pendulum Motion’)
plt.xlabel(‘Time (s)’)
plt.ylabel(‘Angle (rad)’)
plt.grid(True)
plt.show()
- Gas Particle Simulation (Ideal Gas Law)
import numpy as np
import matplotlib.pyplot as plt
# Parameters
num_particles = 100
timesteps = 1000
dt = 0.01
box_size = 10
# Initialize positions and velocities
positions = np.random.rand(num_particles, 2) * box_size
velocities = np.random.randn(num_particles, 2)
# Simulation loop
for t in range(timesteps):
positions += velocities * dt
# Reflecting boundaries
mask_x = (positions[:, 0] < 0) | (positions[:, 0] > box_size)
mask_y = (positions[:, 1] < 0) | (positions[:, 1] > box_size)
velocities[mask_x, 0] *= -1
velocities[mask_y, 1] *= -1
# Visualization
if t % 10 == 0:
plt.clf()
plt.scatter(positions[:, 0], positions[:, 1], c=’blue’)
plt.xlim(0, box_size)
plt.ylim(0, box_size)
plt.title(f’Timestep {t}’)
plt.pause(0.01)
plt.show()
- Electric Field of Point Charges
import numpy as np
import matplotlib.pyplot as plt
# Parameters
k = 8.99e9 # Coulomb’s constant (Nm^2/C^2)
q1 = 1e-9 # Charge 1 (C)
q2 = -1e-9 # Charge 2 (C)
r1 = np.array([0.3, 0.3]) # Position of charge 1
r2 = np.array([-0.3, -0.3]) # Position of charge 2
# Create a grid of points
x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)
# Compute electric field components
def electric_field(q, r0, x, y):
rx = x – r0[0]
ry = y – r0[1]
r = np.sqrt(rx**2 + ry**2)
Ex = k * q * rx / r**3
Ey = k * q * ry / r**3
return Ex, Ey
Ex1, Ey1 = electric_field(q1, r1, X, Y)
Ex2, Ey2 = electric_field(q2, r2, X, Y)
Ex = Ex1 + Ex2
Ey = Ey1 + Ey2
# Plot electric field lines
plt.streamplot(X, Y, Ex, Ey, color=np.sqrt(Ex**2 + Ey**2), linewidth=1, cmap=’cool’)
plt.scatter([r1[0], r2[0]], [r1[1], r2[1]], c=’red’, s=100)
plt.title(‘Electric Field of Point Charges’)
plt.xlabel(‘x’)
plt.ylabel(‘y’)
plt.colorbar(label=’Electric field strength’)
plt.show()
Innovative Physics Simulations
It is approachable to utilize particular tools and libraries for highly intricate simulations:
- VPython: For 3D simulations and visualizations, it is more effective.
- PyBullet: To simulate firm body dynamics, PyBullet is highly appropriate.
- Lattice Boltzmann Method (LBM): It is typically utilized for the simulations of fluid dynamics.
Physics simulation python Project Topics
Python is examined as an efficient programming language that is extensively employed in physics simulation-based projects. By emphasizing physics simulations, we list out 50 significant project topics, which can be implemented through the use of Python:
- Simple Harmonic Oscillator
- Outline: To analyze basic harmonic movement, such as speed, velocity, and displacement, a mass-spring framework has to be simulated.
- Major Tools: Matplotlib and NumPy.
- Projectile Motion
- Outline: In the impact of gravity and preliminary velocity, the direction of a projectile must be designed.
- Major Tools: Matplotlib and NumPy.
- Pendulum Motion
- Outline: As a means to examine periodic activity of a simple pendulum, we simulate its movement.
- Major Tools: SciPy, NumPy, and Matplotlib.
- Double Pendulum
- Outline: Consider a double pendulum framework and design its chaotic movement.
- Major Tools: Matplotlib, NumPy, and SciPy.
- Wave Propagation
- Outline: In various settings, the distribution of waves should be simulated. It could encompass water and sound waves.
- Major Tools: Matplotlib and NumPy.
- Electromagnetic Wave Simulation
- Outline: By means of Maxwell’s equations, the activity of electromagnetic waves has to be designed.
- Major Tools: Matplotlib and NumPy.
- Diffusion Simulation
- Outline: The procedure of diffusion in liquids or gases must be simulated. For that, we utilize random walk models.
- Major Tools: Matplotlib and NumPy.
- Heat Conduction
- Outline: Our project intends to implement the heat equation to design heat transmission in solids.
- Major Tools: Matplotlib and NumPy.
- Solar System Simulation
- Outline: For the solar system, we plan to develop a simulation to analyze gravitational communications and planetary paths.
- Major Tools: VPython, Matplotlib, and NumPy.
- Black Hole Simulation
- Outline: Across a black hole, the gravitational field should be designed. In that area, consider the path of objects.
- Major Tools: Matplotlib and NumPy.
- Fluid Dynamics using SPH
- Outline: Through Smoothed Particle Hydrodynamics (SPH) techniques, we simulate the flow of fluids.
- Major Tools: Matplotlib and NumPy.
- Lennard-Jones Potential
- Outline: To analyze molecular dynamics, the communications among particles have to be simulated with the Lennard-Jones potential.
- Major Tools: Matplotlib and NumPy.
- Quantum Harmonic Oscillator
- Outline: By utilizing the Schrodinger equation, the activity of a quantum harmonic oscillator has to be simulated.
- Major Tools: Matplotlib and NumPy.
- Monte Carlo Simulations
- Outline: In order to simulate statistical physics problems such as the Ising model, our project implements Monte Carlo techniques.
- Major Tools: Matplotlib and NumPy.
- Electric Field of Point Charges
- Outline: The electric field must be visualized, which is specifically produced by several point charges.
- Major Tools: Matplotlib and Numpy.
- Magnetic Field Simulation
- Outline: In this project, the magnetic field has to be simulated, which is produced by magnets or current-carrying wires.
- Major Tools: Matplotlib and NumPy.
- Circuit Simulation
- Outline: With Kirchhoff’s laws, we aim to design electrical circuits. Then, their activity should be simulated.
- Major Tools: Matplotlib and NumPy.
- Fluid Flow in Pipes
- Outline: Across pipes, consider the fluid flow and simulate it. Various aspects such as turbulence and viscosity must be analyzed.
- Major Tools: Matplotlib and NumPy.
- Rocket Trajectory
- Outline: In the impact of air resistance, gravity, and thrust, examine the direction of a rocket and design it.
- Major Tools: Matplotlib and NumPy.
- Relativity Simulation
- Outline: Different relativistic impacts have to be simulated. It could include length contraction and time dilation.
- Major Tools: Matplotlib and NumPy.
- Wave-Particle Duality
- Outline: By means of the double-slit trial, the wave-particle duality should be visualized.
- Major Tools: Matplotlib and Numpy.
- Buoyancy and Archimedes’ Principle
- Outline: The buoyant force has to be simulated, which is exhibited on objects in fluids.
- Major Tools: Matplotlib and NumPy.
- Optics and Lenses
- Outline: Examine the light when it passes across mirrors and lenses, and design its activity.
- Major Tools: Matplotlib and NumPy.
- Thermal Radiation
- Outline: On the basis of temperature, we consider the discharge of thermal radiation from objects and simulate it.
- Major Tools: Matplotlib and NumPy.
- Solar Energy Simulation
- Outline: With photovoltaic cells, the gathering and transformation of solar energy must be designed.
- Major Tools: Matplotlib and NumPy.
- Crystallography
- Outline: Focus on crystal lattices and simulate their development and features.
- Major Tools: Matplotlib and NumPy.
- Brownian Motion
- Outline: The random motion of particles has to be designed, which are mixed in a fluid.
- Major Tools: Matplotlib and NumPy.
- Projectile Motion with Air Resistance
- Outline: As a means to encompass air resistance, the simple projectile motion framework should be expanded.
- Major Tools: Matplotlib and NumPy.
- Tsunami Simulation
- Outline: In oceans, the creation and distribution of tsunamis must be designed.
- Major Tools: Matplotlib and NumPy.
- Chaos Theory and Lorenz Attractor
- Outline: To analyze chaos concept, we intend to simulate chaotic frameworks such as the Lorenz attractor.
- Major Tools: Matplotlib and NumPy.
- Seismic Wave Propagation
- Outline: Across the Earth’s layers, consider the distribution of seismic waves and simulate it.
- Major Tools: Matplotlib and NumPy.
- Wind Turbine Simulation
- Outline: Along with the energy generation, the behavior of wind turbines has to be designed.
- Major Tools: Matplotlib and NumPy.
- Traffic Flow Simulation
- Outline: On roads, the traffic flow should be simulated. Then, focus on examining congestion trends.
- Major Tools: Matplotlib and NumPy.
- Hydrodynamics
- Outline: In movement, the fluid dynamics have to be designed. It could encompass turbulent flow and laminar.
- Major Tools: Matplotlib and NumPy.
- Energy Transfer in Ecosystems
- Outline: Across various trophic levels in an environment, we examine the energy flow and simulate it.
- Major Tools: Matplotlib and Numpy.
- Nuclear Decay Simulation
- Outline: The decay of radioactive isotopes has to be designed. Then, plan to analyze half-life.
- Major Tools: Matplotlib and NumPy.
- Particle in a Box
- Outline: Consider a particle enclosed in a box and simulate its quantum mechanical activity.
- Major Tools: Matplotlib and NumPy.
- Kinetic Theory of Gases
- Outline: Through the concepts of kinetic theory, we design the activity of gases.
- Major Tools: Matplotlib and NumPy.
- Galactic Collision Simulation
- Outline: Concentrate on galaxies and design their communication and collision.
- Major Tools: Matplotlib and NumPy.
- Meteor Impact Simulation
- Outline: On planetary regions, the effect of meteors has to be simulated.
- Major Tools: Matplotlib and NumPy.
- Surface Tension Simulation
- Outline: In liquid droplets, examine the impacts of surface tension and design it.
- Major Tools: Matplotlib and NumPy.
- Diffraction and Interference Patterns
- Outline: Consider light waves and simulate their interference and diffraction.
- Major Tools: Matplotlib and NumPy.
- Capillary Action
- Outline: Specifically in narrow tubes, the capillary flow of liquids has to be designed.
- Major Tools: Matplotlib and NumPy.
- Electron Transport in Semiconductors
- Outline: In semiconductor materials, examine the motion of electrons and simulate it.
- Major Tools: Matplotlib and NumPy.
- Magnetic Resonance Imaging (MRI) Simulation
- Outline: To visualize internal parts, we plan to design the concepts of MRI.
- Major Tools: Matplotlib and NumPy.
- Tidal Forces Simulation
- Outline: On planetary objects, consider the impacts of tidal forces and design it.
- Major Tools: Matplotlib and NumPy.
- Snowflake Formation Simulation
- Outline: From water vapor, the creation of snowflakes must be simulated.
- Major Tools: Matplotlib and NumPy.
- Lightning Formation
- Outline: The physical operations have to be designed, which creates lightning.
- Major Tools: Matplotlib and NumPy.
- Particle Swarm Optimization
- Outline: With the aim of resolving intricate optimization issues, we apply particle swarm optimization techniques.
- Major Tools: Matplotlib and NumPy.
- Acoustic Wave Simulation
- Outline: In various settings, the distribution of sound waves has to be designed.
- Major Tools: Matplotlib and NumPy.
As a means to carry out physics simulations with Python, we recommended some significant approaches and instances in an explicit manner. Related to physics simulations, several Python project topics are proposed by us, along with concise explanations and major tools.
Subscribe Our Youtube Channel
You can Watch all Subjects Matlab & Simulink latest Innovative Project Results
Our services
We want to support Uncompromise Matlab service for all your Requirements Our Reseachers and Technical team keep update the technology for all subjects ,We assure We Meet out Your Needs.
Our Services
- Matlab Research Paper Help
- Matlab assignment help
- Matlab Project Help
- Matlab Homework Help
- Simulink assignment help
- Simulink Project Help
- Simulink Homework Help
- Matlab Research Paper Help
- NS3 Research Paper Help
- Omnet++ Research Paper Help
Our Benefits
- Customised Matlab Assignments
- Global Assignment Knowledge
- Best Assignment Writers
- Certified Matlab Trainers
- Experienced Matlab Developers
- Over 400k+ Satisfied Students
- Ontime support
- Best Price Guarantee
- Plagiarism Free Work
- Correct Citations
Expert Matlab services just 1-click

Delivery Materials
Unlimited support we offer you
For better understanding purpose we provide following Materials for all Kind of Research & Assignment & Homework service.
 Programs
Programs Designs
Designs Simulations
Simulations Results
Results Graphs
Graphs Result snapshot
Result snapshot Video Tutorial
Video Tutorial Instructions Profile
Instructions Profile  Sofware Install Guide
Sofware Install Guide Execution Guidance
Execution Guidance  Explanations
Explanations Implement Plan
Implement Plan
Matlab Projects
Matlab projects innovators has laid our steps in all dimension related to math works.Our concern support matlab projects for more than 10 years.Many Research scholars are benefited by our matlab projects service.We are trusted institution who supplies matlab projects for many universities and colleges.
Reasons to choose Matlab Projects .org???
Our Service are widely utilized by Research centers.More than 5000+ Projects & Thesis has been provided by us to Students & Research Scholars. All current mathworks software versions are being updated by us.
Our concern has provided the required solution for all the above mention technical problems required by clients with best Customer Support.
- Novel Idea
- Ontime Delivery
- Best Prices
- Unique Work
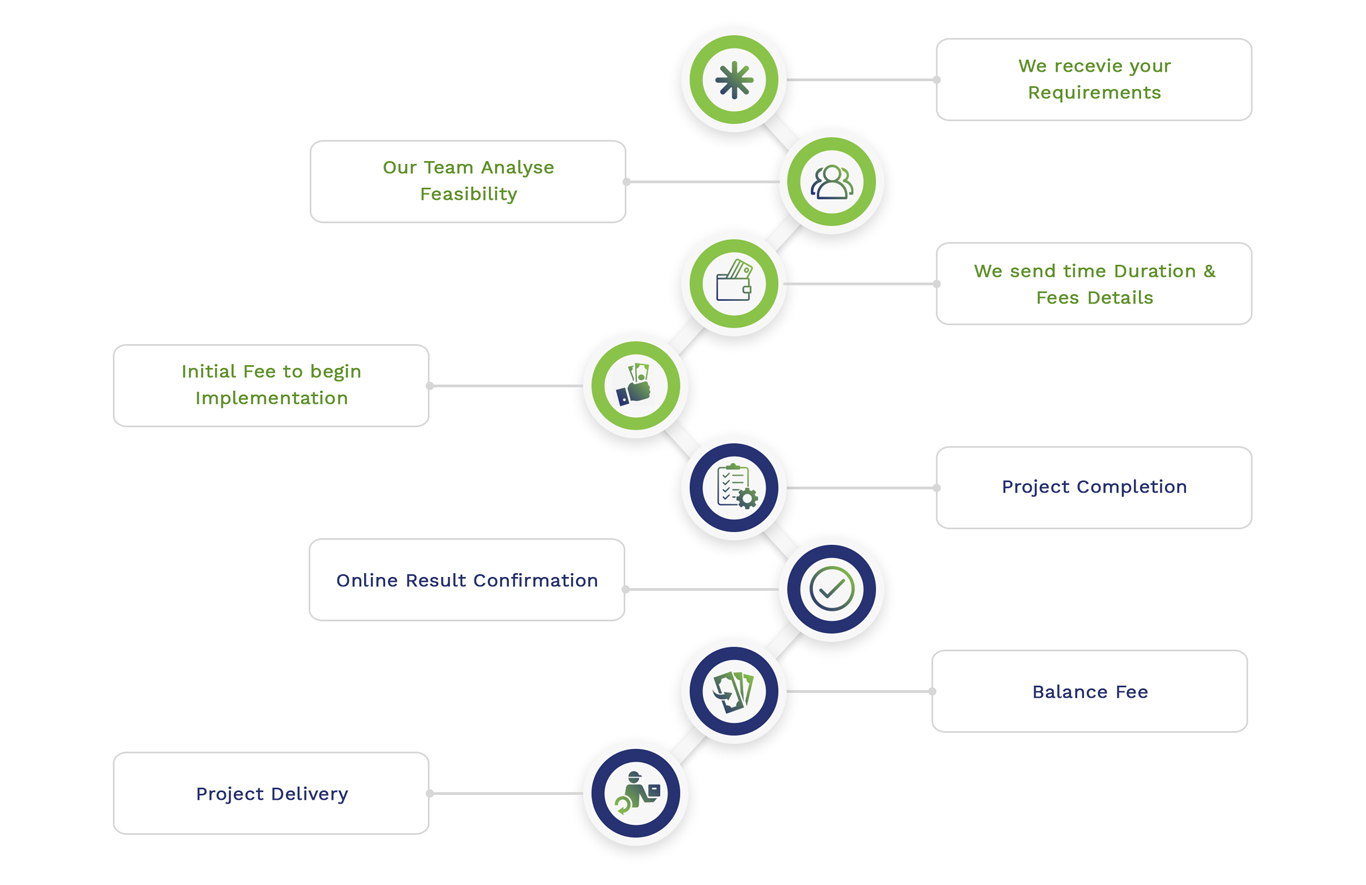
Simulation Projects Workflow
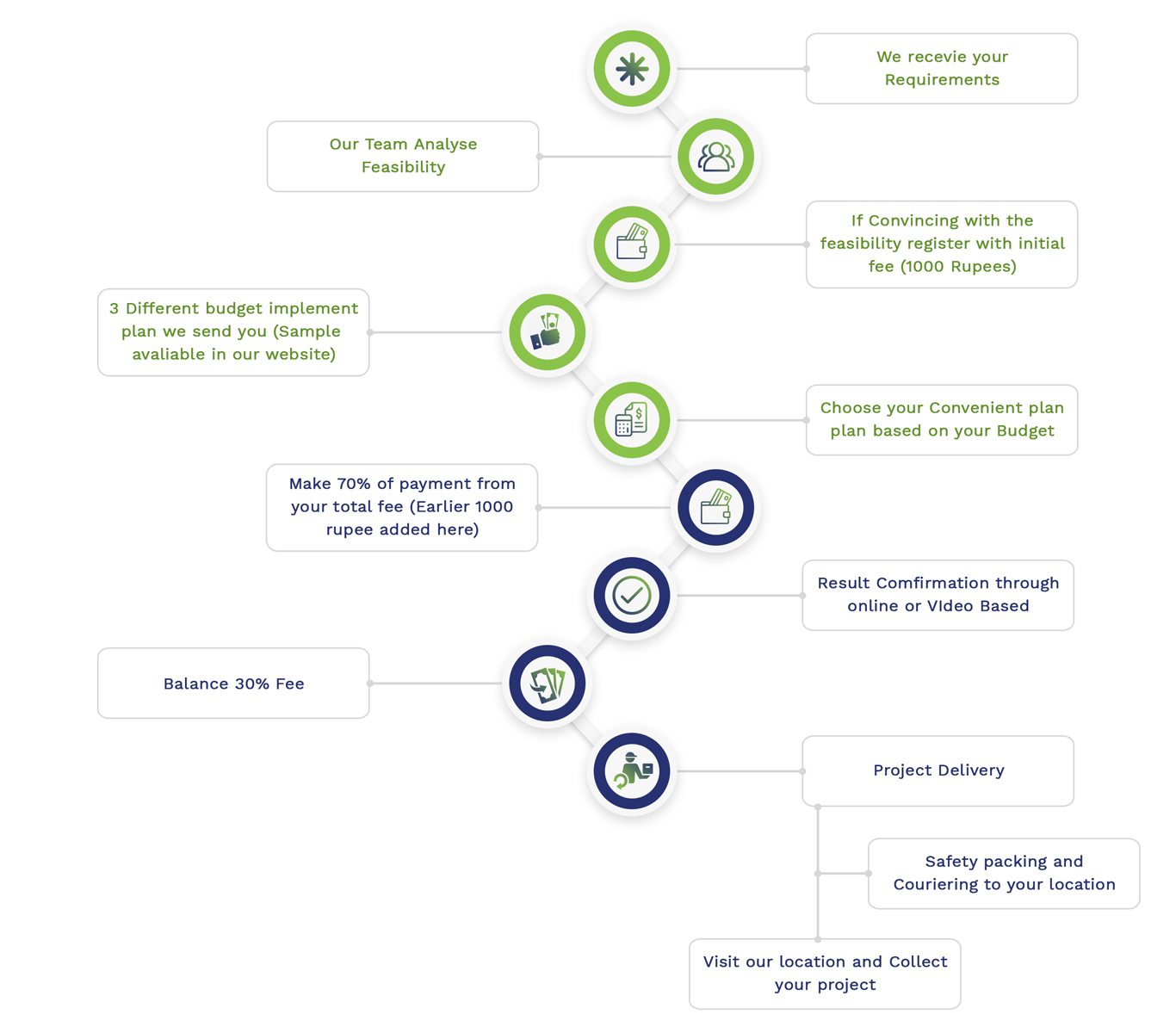
Embedded Projects Workflow


 Matlab
Matlab Simulink
Simulink NS3
NS3 OMNET++
OMNET++ COOJA
COOJA CONTIKI OS
CONTIKI OS NS2
NS2






