LMS Algorithm MATLAB projects are worked by us; by sharing all your project details with us we will take your project to next level of success, as we have more than 100+ trained researchers working for your project. Get your research article done from hand of our writers. Applying the LMS (Least Mean Squares) algorithm in MATLAB is considered as a challenging process that must be carried out in an appropriate manner by following several guidelines. To apply the LMS algorithm in MATLAB, we provide an in-depth instruction in an explicit way:
Procedural Instruction
- Specify the Issue
Initially, it is significant to consider that we have an input signal x(n) and an expected signal d(n). Modifying the filter coefficients adaptively to reduce the error e(n) = d(n) – y(n) is the major aim of the LMS algorithm. Here, the result of the adaptive filter is indicated as y(n).
- Set Parameters
For step size (learning rate), filter coefficients, and other major parameters, initialize the preliminary states.
- Apply the LMS Algorithm
By utilizing the LMS algorithm formula, we need to upgrade the filter coefficients in an iterative manner.
MATLAB Implementation
To apply the LMS algorithm in MATLAB, we offer a basic instance of code:
% Parameters
N = 1000; % Number of samples
mu = 0.01; % Step size (learning rate)
filterOrder = 4; % Number of filter coefficients
% Generate synthetic input and desired signals
x = randn(1, N); % Input signal (e.g., white noise)
d = filter([0.5, -0.5, 0.3, -0.3], 1, x) + 0.1*randn(1, N); % Desired signal
% Initialize filter coefficients and other variables
w = zeros(filterOrder, 1); % Filter coefficients
y = zeros(1, N); % Output signal
e = zeros(1, N); % Error signal
% LMS algorithm
for n = filterOrder:N
x_n = x(n:-1:n-filterOrder+1)’; % Input vector
y(n) = w’ * x_n; % Filter output
e(n) = d(n) – y(n); % Error signal
w = w + mu * x_n * e(n); % Update filter coefficients
end
% Plot the results
figure;
subplot(3, 1, 1);
plot(d);
title(‘Desired Signal’);
xlabel(‘Sample Number’);
ylabel(‘Amplitude’);
subplot(3, 1, 2);
plot(y);
title(‘Output Signal’);
xlabel(‘Sample Number’);
ylabel(‘Amplitude’);
subplot(3, 1, 3);
plot(e);
title(‘Error Signal’);
xlabel(‘Sample Number’);
ylabel(‘Amplitude’);
Description
- Parameters:
- N denotes the total number of samples.
- The learning rate or step size is indicated as mu. The convergence speed of the algorithm is regulated by this parameter.
- filterOrder specifies the total amount of filter coefficients.
- Generate Synthetic Signals:
- The variable x signifies the input signal (for instance: white noise).
- The expected signal is indicated as d. Through appending some noise and passing the input signal via a predetermined filter, this expected signal is generally produced.
- Initialize Variables:
- For the vector of filter coefficients, we use the variable w, which is set to zero.
- y denotes the output signal.
- The error signal is signified as e.
- LMS Algorithm:
- For upgrading the filter coefficients at every step, the algorithm repeats through the input signal.
- Specifically for every sample, w is upgraded in terms of the current input and error, y(n) indicates the filter output, x_n denotes the current input vector, and e(n) signifies the error signal.
- Plot the Outcomes:
- In order to visualize the performance of the LMS algorithm, various aspects are plotted, such as expected signal, output signal, and error signal.
Supplementary Aspects
- Step Size (Learning Rate): It is more important to select the appropriate step size. A huge mu can result in imbalance but may generate rapid convergence, and the small mu assures balanced convergence but in a slower manner.
- Filter Order: The capacity and intricateness of the adaptive filter is fixed by the filter order. A greater order needs high computations for designing highly complicated frameworks.
- Performance Metrics: By considering different metrics like convergence speed and Mean Squared Error (MSE), the performance of the LMS algorithm can be assessed.
Top 50 lms algorithm project topics
LMS (Least Mean Squares) is referred to as an efficient algorithm that is widely considered in several latest research projects. Relevant to the LMS algorithm, we list out 50 major project topics, which involves a vast amount of applications in communications, control systems, adaptive filtering, signal processing, and other significant areas:
Signal Processing and Adaptive Filtering
- Adaptive Echo Cancellation in Telecommunication Systems
- Adaptive Equalization for Digital Communication Channels
- Adaptive Beamforming for Smart Antennas
- Adaptive Line Enhancer for Narrowband Interference Suppression
- Adaptive Filtering for Seismic Signal Processing
- Adaptive Noise Cancellation in Audio Signals using LMS
- Real-Time Signal Enhancement for Hearing Aids using LMS Algorithm
- Active Noise Control in Headphones using LMS Algorithm
- Adaptive Filtering for ECG Signal Denoising
- Adaptive Channel Estimation in Wireless Communication
Control Systems
- Adaptive Control for Inverted Pendulum System
- Temperature Control in HVAC Systems using LMS
- Adaptive Filtering for Robot Path Planning
- Wind Turbine Control using Adaptive Filtering Techniques
- Adaptive Control of Magnetic Levitation Systems
- Adaptive Control of DC Motors using LMS Algorithm
- Adaptive Cruise Control in Autonomous Vehicles
- Adaptive Vibration Control in Mechanical Structures
- Adaptive Control of Hydraulic Systems
- Adaptive Control for Smart Grid Systems
Image Processing
- Adaptive Image Restoration for Blurred Images
- Adaptive Edge Detection using LMS Filtering
- Adaptive Image Denoising using LMS Algorithm
- Adaptive Filtering for Image Compression
- Noise Reduction in Medical Imaging using LMS
Communications
- Adaptive Beamforming for MIMO Systems
- Adaptive Power Control in Wireless Networks
- Adaptive Equalization for OFDM Systems
- Interference Cancellation in Cognitive Radio Networks
- Channel Estimation in 5G Networks using LMS
Financial Applications
- Noise Reduction in Financial Time Series Data
- Predictive Modeling for Cryptocurrency Markets using LMS
- Adaptive Filtering for Stock Price Prediction
- Adaptive Risk Management Strategies using LMS
Biomedical Applications
- Real-Time Blood Pressure Monitoring using LMS
- Adaptive Control in Prosthetic Devices
- Adaptive Filtering for EEG Signal Analysis
- Adaptive Filtering for Heart Rate Variability Analysis
Audio and Speech Processing
- Noise Reduction in Mobile Communication
- Real-Time Speech Enhancement using LMS Algorithm
- Echo Cancellation in VoIP Systems
- Adaptive Filtering for Speech Recognition Systems
Environmental and Industrial Applications
- Adaptive Filtering for Air Quality Monitoring
- Adaptive Control of Water Treatment Processes
- Noise Reduction in Industrial Machinery
- Adaptive Filtering for Environmental Data Analysis
Machine Learning and Data Analysis
- Noise Reduction in Sensor Networks using LMS
- Adaptive Feature Selection for Machine Learning Models
- Predictive Maintenance in Industrial Systems using LMS
- Adaptive Filtering for Big Data Analytics
Instance: Adaptive Noise Cancellation in Audio Signals using LMS
Step 1: Specify the Issue
On the basis of the LMS algorithm, the noise has to be eliminated from an audio signal with an adaptive noise cancellation framework.
Step 2: Load and Preprocess the Data
% Load audio signal (desired signal)
[desiredSignal, Fs] = audioread(‘clean_audio.wav’);
% Load noise signal
[noiseSignal, ~] = audioread(‘noise.wav’);
% Mix noise with the desired signal to create the noisy signal
noisySignal = desiredSignal + noiseSignal;
% Plot the signals
figure;
subplot(3, 1, 1);
plot(desiredSignal);
title(‘Clean Audio Signal’);
subplot(3, 1, 2);
plot(noiseSignal);
title(‘Noise Signal’);
subplot(3, 1, 3);
plot(noisySignal);
title(‘Noisy Audio Signal’);
Step 3: For noise elimination, apply the LMS algorithm.
% Parameters
mu = 0.01; % Step size
filterOrder = 32; % Number of filter coefficients
% Initialize filter coefficients
w = zeros(filterOrder, 1);
% Initialize variables
N = length(noisySignal);
y = zeros(N, 1);
e = zeros(N, 1);
% Adaptive noise cancellation using LMS
for n = filterOrder:N
x = noiseSignal(n:-1:n-filterOrder+1);
y(n) = w’ * x;
e(n) = noisySignal(n) – y(n);
w = w + mu * x * e(n);
end
% Plot the results
figure;
subplot(2, 1, 1);
plot(noisySignal);
title(‘Noisy Audio Signal’);
subplot(2, 1, 2);
plot(e);
title(‘Cleaned Audio Signal using LMS’);
Step 4: Examine the Outcomes
Through contrasting the actual clean audio signal with the cleaned signal, we have to assess the performance. For that, consider various metrics like Mean Squared Error (MSE) or Signal-to-Noise Ratio (SNR).
Step 5: Documentation and Presentation
- By encompassing the problem description, methodology, outcomes, and deployment, create a document.
- The major discoveries have to be depicted. For noise elimination, the efficiency of the LMS algorithm must be examined.
For applying the LMS algorithm in MATLAB, procedural instruction is offered by us in an in-depth manner, along with concise descriptions and supplementary aspects. In addition to that, we recommended LMS algorithm-based project topics by including several applications in various domains. We work on all areas of LMS Algorithm MATLAB, and provide you with best implementation support. Contact us to get immediate support on LMS Algorithm MATLAB.
Subscribe Our Youtube Channel
You can Watch all Subjects Matlab & Simulink latest Innovative Project Results
Our services
We want to support Uncompromise Matlab service for all your Requirements Our Reseachers and Technical team keep update the technology for all subjects ,We assure We Meet out Your Needs.
Our Services
- Matlab Research Paper Help
- Matlab assignment help
- Matlab Project Help
- Matlab Homework Help
- Simulink assignment help
- Simulink Project Help
- Simulink Homework Help
- Matlab Research Paper Help
- NS3 Research Paper Help
- Omnet++ Research Paper Help
Our Benefits
- Customised Matlab Assignments
- Global Assignment Knowledge
- Best Assignment Writers
- Certified Matlab Trainers
- Experienced Matlab Developers
- Over 400k+ Satisfied Students
- Ontime support
- Best Price Guarantee
- Plagiarism Free Work
- Correct Citations
Expert Matlab services just 1-click

Delivery Materials
Unlimited support we offer you
For better understanding purpose we provide following Materials for all Kind of Research & Assignment & Homework service.
 Programs
Programs Designs
Designs Simulations
Simulations Results
Results Graphs
Graphs Result snapshot
Result snapshot Video Tutorial
Video Tutorial Instructions Profile
Instructions Profile  Sofware Install Guide
Sofware Install Guide Execution Guidance
Execution Guidance  Explanations
Explanations Implement Plan
Implement Plan
Matlab Projects
Matlab projects innovators has laid our steps in all dimension related to math works.Our concern support matlab projects for more than 10 years.Many Research scholars are benefited by our matlab projects service.We are trusted institution who supplies matlab projects for many universities and colleges.
Reasons to choose Matlab Projects .org???
Our Service are widely utilized by Research centers.More than 5000+ Projects & Thesis has been provided by us to Students & Research Scholars. All current mathworks software versions are being updated by us.
Our concern has provided the required solution for all the above mention technical problems required by clients with best Customer Support.
- Novel Idea
- Ontime Delivery
- Best Prices
- Unique Work
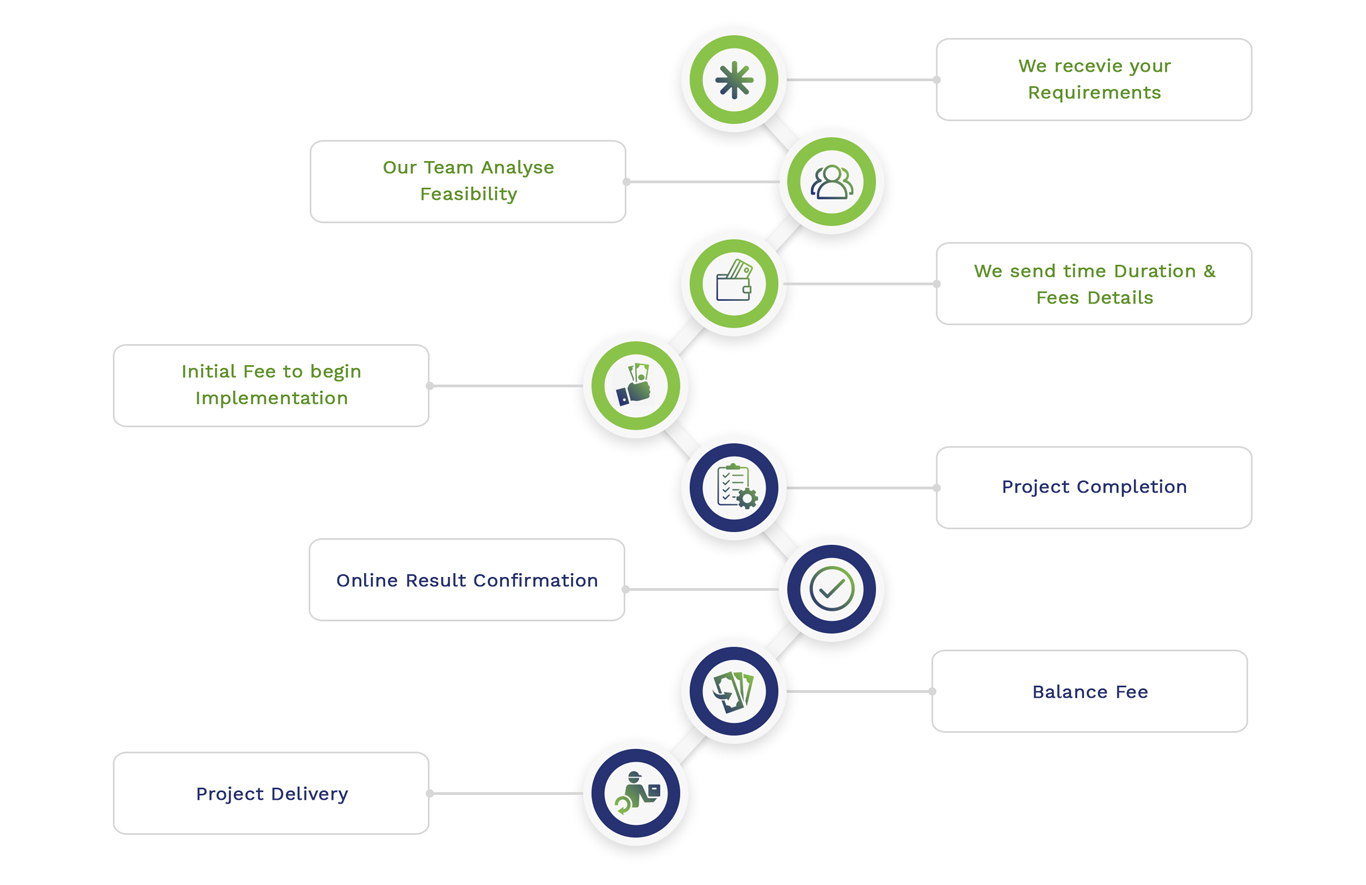
Simulation Projects Workflow
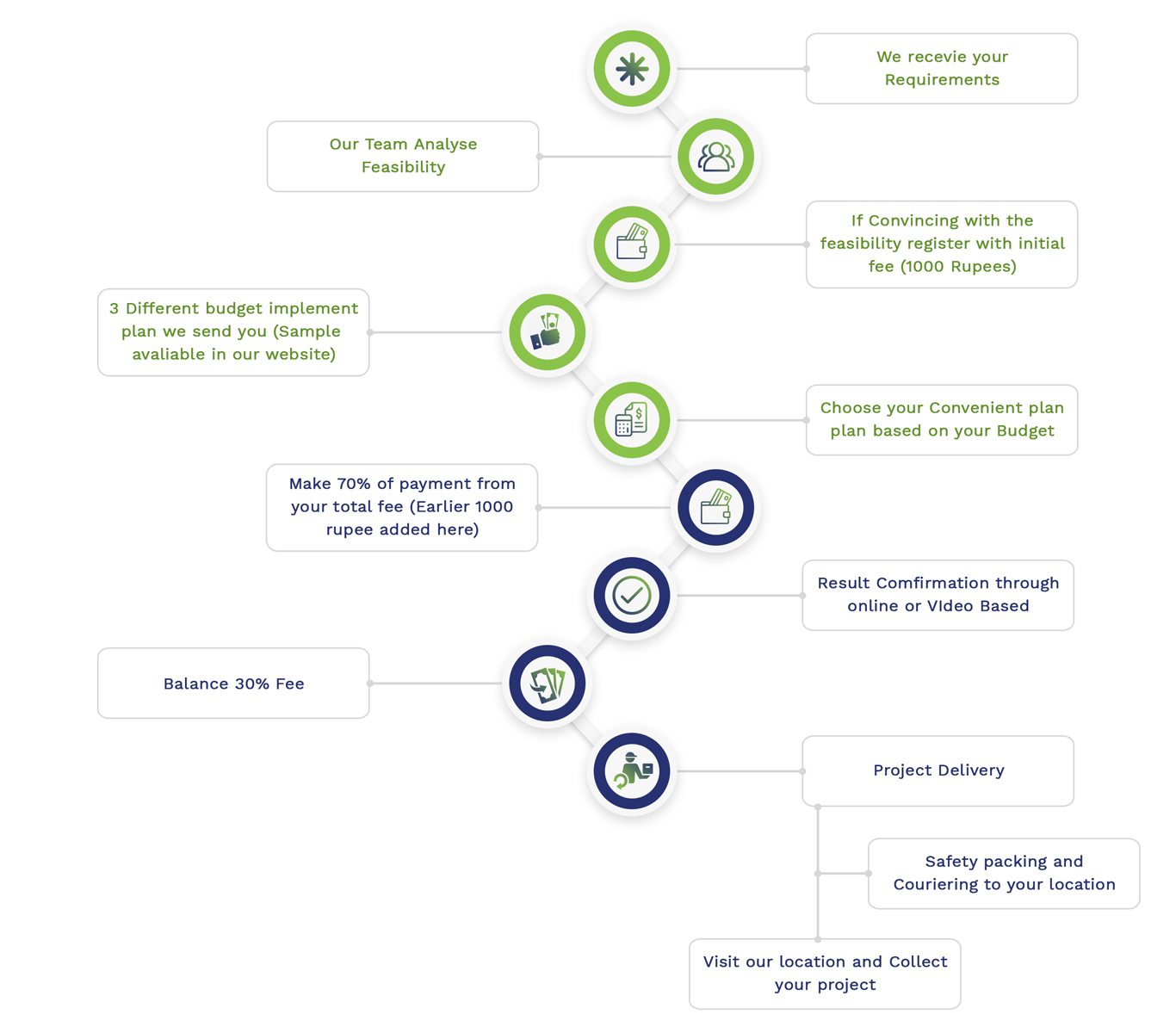
Embedded Projects Workflow


 Matlab
Matlab Simulink
Simulink NS3
NS3 OMNET++
OMNET++ COOJA
COOJA CONTIKI OS
CONTIKI OS NS2
NS2






